কেন্দ্রমুখী ত্বরণ, স্পর্শী ত্বরণ এবং কৌণিক ত্বরণ-এর মধ্যে পার্থক্য কী?
কেন্দ্রমুখী ত্বরণ, স্পর্শী ত্বরণ এবং কৌণিক ত্বরণ-এর মধ্যে পার্থক্য কী?
শূন্য বা শূন্যের কাছাকাছি সময় ব্যাবধানে, কেন্দ্র স্থির রেখে কোনো বস্তু চক্রাকারে ঘূর্ণনশীল হলে, বস্তুর কেন্দ্র অভিমুখে যে প্রযুক্ত বেগ বৃদ্ধির হার সৃষ্টির হয়, তাকে কেন্দ্রমুখী ত্বরণ বলে। যা a দ্বারা প্রকাশিত। এর সূত্রটি হলো a=(v^2)/r। v=ঘূর্ণনবেগ, r=ঘূর্ণন চক্রের কেন্দ্র থেকে ব্যাসার্ধ কোন সমতলে চলা বস্তুর দ্রুতির পরিবর্তনকে স্পর্শকীয় ত্বরণ বলে।
কৌণিক ত্বরণ হল সময়ের সাথে কোনো অক্ষের চতুর্দিকে ঘূর্নায়মান কোন বস্তুর বা বিন্দুর কৌণিক বেগের পরিবর্তনের হার। a (আলফা) দ্বারা প্রকাশ করে। এটি সাধারণ ত্বরণেরই ভেক্টর রাশি। অর্থাৎ এর দিক নির্দিষ্ট।
এখানে, মূল যে পার্থক্যটি পরিলক্ষিত হচ্ছে, তা হলো- তিনটি ত্বরণের কাজ তিন রকম।এর মধ্যে
১। কেন্দ্রমুখী ও স্পর্শী ত্বরণটি স্কেলার রাশি এবং কৌণিক ত্বরণ ভেক্টর রাশি।
২। স্পর্শী ত্বরণের ক্ষেত্রে তলটি অবশ্যই সমতল অর্থাৎ সুষম পৃষ্ঠ হতে হবে। বাকি দুটি যেকোনো পৃষ্ঠেই প্রযোজ্য।
৩। কেন্দ্রমুখী ত্বরণই শুধুমাত্র কেন্দ্রের দিকে একটি বল অনুভব করে।অপর দুটির ক্ষেত্রে এই বল মুখ্য নয়।
৪। কৌণিক ত্বরণ সবসময় অক্ষ বরাবর কাজ করবে। অক্ষ নির্দিষ্ট না করে সেটি কৌণিক ত্বরণ বলা যাবে না।
৫। কেন্দ্রমুখী ত্বরণ নির্ণয়ে অতি ক্ষুদ্র সময়ের ব্যবধানকে বিবেচনা করতে হয়। কৌণিক ত্বরণ প্রতি একক সময়ের ব্যবধানকে বিবেচনা করতে হয়।
রৈখিক বেগের কার্ল, কৌণিক বেগের দ্বিগুণ কেমন করে?
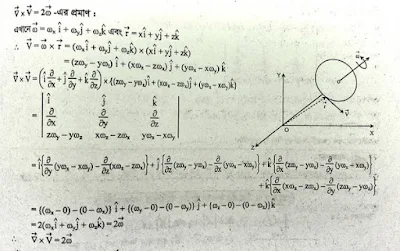 |
কৌণিক কম্পাঙ্ক কাকে বল?
সময়ের সাথে তরঙ্গের ওপর অবস্থিত কোনো কণার দশার পরিবর্তনের হারকে ঐ তরঙ্গের কৌণিক কম্পাঙ্ক বলে।
কৌণিক কম্পাঙ্ক ও কৌণিক বেগ কেন একই?
যদিও সাঙ্কেতিক অর্থে দুটো একই, অর্থাৎ দুটোই ওমেগা দিয়ে প্রকাশ হয়, তবে সামান্য পার্থক্য রয়েছে।
ω(omega)= (2π÷T) =2πf
এখানে W(omega)= কৌণিক কম্পাঙ্ক, f= কম্পাঙ্ক, T= পর্যায়কাল। এই কৌণিক কম্পাঙ্ক দ্বারা বুঝায়, যেকোনো ঘূর্ণনশীল বস্তু একবার ঘুরে আসতে (অর্থাৎ, একটি বৃত্ত পথ সম্পন্ন করতে) যে পরিমাণ কম্পন সৃষ্টি করে।
কৌণিক বেগ বলতে, কোনো নির্দিষ্ট কোণে বৃত্তাকার পথে ঘূর্ণায়মান বস্তু যখন ক্ষুদ্রাতিক্ষুদ্র সময়ের ব্যবধানে নির্দিষ্ট সরণ উৎপন্ন করার গতিকে কৌণিক বেগ বলে।
ω(omega)=কৌণিক বেগ =θ/t
এখন, অনেক ক্ষেত্রে, কৌণিক কম্পাঙ্ক নির্ণয়ে বেগের সূত্রটি ব্যবহার করতে দেখা যায়। এবং এটি অবশ্যই সঠিক। কিন্তু এটি তখনই সঠিক যখন বৃত্তাকার পথে একবার ঘুরে আসার নির্দিষ্ট সময় উল্লেখ করা থাকে, অর্থাৎ, T বা পর্যায়কাল উল্লেখ করা থাকে। কৌণিক কম্পাঙ্কে তা থাকবেই। কারণ মূলত, কৌণিক কম্পাংক নির্ণয়ে একটি কম্পনশীল বস্তুর কম্পাঙ্কই নির্ণয় করা হচ্ছে, যা বৃত্তাকার পথে ঘূর্ণনরত আছে। একটি বৃত্তপথ সম্পন্ন করতে যত কম্পন হতে পারে, সেই পরিমাণ।আর, কৌণিক বেগ নির্ভর করে, যেকোনো ক্ষুদ্রাতিক্ষুদ্র সময়ের ব্যবধানে ঘূর্ণশীল বস্তুর গতি।
কৌণিক কম্পাঙ্কের ক্ষেত্রে W^2=k/m হয় কিভাবে?
কৌণিক কম্পাঙ্ক বা যাকে ইংলিশ এ বলে angular frequency এই বিষয়টির প্রয়োজন পরে কোনো periodic motion এর জন্য , সেটা সরল দোলগতি হতেও পারে নাও হতে পারে । angular frequency হলো কোনো কণা বা বস্তু 1 সেকেন্ডে কত রেডিয়ান কোণ অতিক্রম করে ,ফলে এর একক হয় rad/sec বা রেডিয়ান প্রতি সেকেন্ড । একটি সম্পূর্ণ ঘূর্ণন হলে বস্তু বা কণাটি 2π রেডিয়ান কোন অতিক্রম করে অর্থাৎ ω = 2π/T
T হলো পর্যায়কাল । এবার আসি মূল এক্সপ্রেশন এ ,কোনো periodic motion ( সেটা simple harmonic হতেই হবে)কে বোঝানোর জন্য differential equation দ্বারা বোঝানো হয়
সরল দোলগতি তে restoring বল কনাটির সরণ এর সমানুপাতি হয় অর্থাৎ F= -kx , k হলো বলধ্রুবক । এবার আমরা নিউটন বলবিদ্যা দিয়ে গতির সমীকরণ তৈরি করি তা ঠিক এইরকম হবে।
এখানে a= acceleration বা ত্বরণ ( যখন কোনো বস্তুর ওপর বল প্রযুক্ত হবে তখন সেখানে ত্বরণ এর সৃষ্টি হবে) ,m = mass of the particle (বস্তুর ভর)
এইখান থেকে যে differential equation তৈরি হয় তাতে √(k/m ) কে কৌণিক কম্পাঙ্ক বলে ,যা সেই নির্দিষ্ট সিস্টেম এর ওপর নির্ভর করে , যেমন একটি কাঠের চোঙ কে জলে সামান্য ডুবিয়ে ছেড়ে দিলে সেটি oscillate করবে তখন সেক্ষেত্রে তার গতির সমীকরণ এইরকম হবে।
এক্ষেত্রে ω এর মান √(Apg/m) অর্থাৎ এটির কৌণিক কম্পাঙ্ক এর মান হবে √(Apg/m) । তাই k এর মান সেই oscillating system এর ওপর নির্ভর করে তার নানান এক্সপ্রেশন হবে ,তবে ω ^2 এর এই এক্সপ্রেশন টা general অর্থাৎ যেকোনো simple harmonic motion এর জন্য প্রযোজ্য ।
রৈখিক ত্বরণ ও কৌণিক ত্বরণের সম্পর্ক কী?
রৈখিক ত্বরণ এবং কৌণিক ত্বরণের সম্পর্ক
a=rαa= রৈখিক ত্বরণr=ঘূর্ণনবিন্দু হতে বিন্দুর দূরত্বα =কৌণিক ত্বরণ
এই রকম আরও তথ্য পেতে আমাদের ফেসবুক পেজে লাইক দিয়ে যুক্ত থাকুন। এর পাশাপাশি গুগল নিউজে আমাদের ফলো করুন।









